问题: 对于任何一个由若干个电阻连接而成的有限电阻网络，如果已知每一个电阻的阻值，能否求得任何两个节点之间的等效电阻?

转化为图论语言

由于对于任何的两个电阻之间的连接关系只会是串联或者是并联，因此可以发现对于电阻的性质和图论中的边的性质非常的像，因此转化为图论的语言
对于电路图G1对应的图G2,G1中的每一个节点，都对应这G2中的一个点，而对于G1中的点A1,A2中有一个电阻R1,那么就是在A1,A2中连上一条边，对于阻值是不用考虑的，因为对于我们的目标就是消去所有的点，形成最后的点N,M之间的一条的边，因此只要考虑对于对于图的操作中的点与边的关系,如

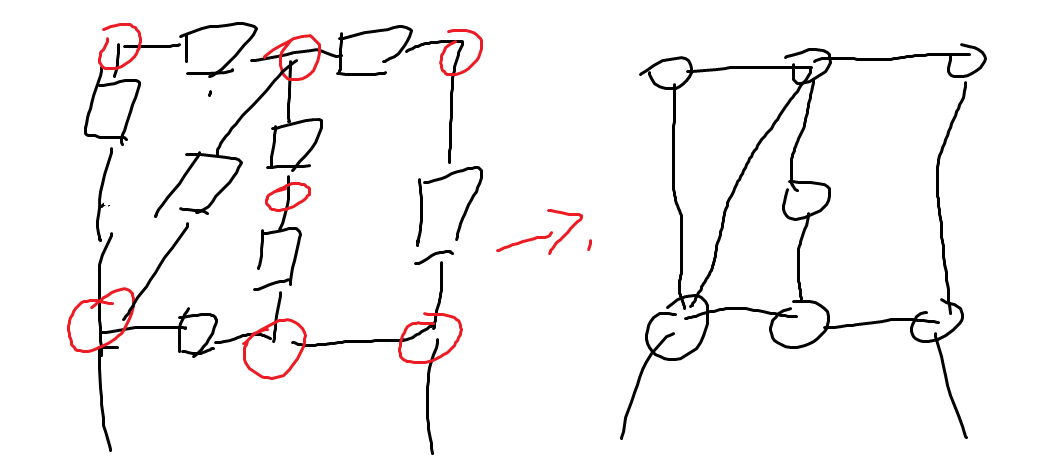
对于串并联，星Y变换

• 对于串联而言，就是如果有两个并排连接的电阻，可以将其阻值加起来， 图论中就是对于任何的一个deg为2的节点A,设其儿子为BC,那么可以将BC之间连起来一条的边，然后将A消去，即为

  G2中每一个点的deg都大于2

• 并联实际上，就是对于两个点之间如果有好多条边，那么可以将他们合并成一条的边，即为

  G2中没有重边

• 对于星Y变换，实际上就是用下面的图片解释

</center>

回到原来的问题

对于原来的图G2由串联关系可以保证对于任何的点的度都是>=3的，而取其中的度最小的哪一个点，重复执行星Y变换，从而当该点无法继续执行该变换的时候有该店要么直接去掉，要么就是由串联消去 总之每一次的这样的操作都可以消去G2中的一个点，从而点的数量会不断的减少，直到不存在满足deg>=3的点，此时只有N,M之间有边，即为用以上的几种的变换就理论上可以解答出所有的电阻网络

是时候该立体机动装置登场了 ——纳拿巴